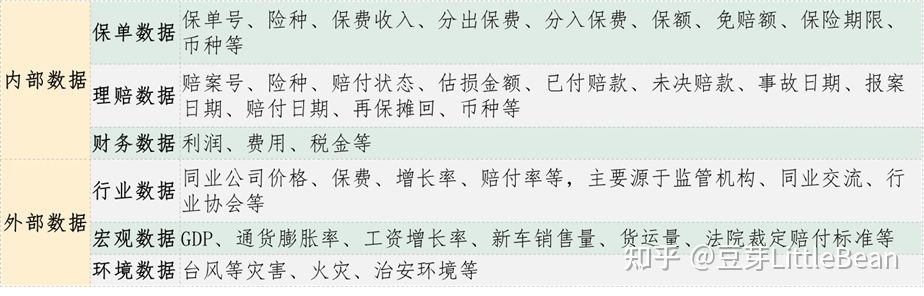
今天总结广义线性模型(GLM :Generalized Linear Models)的原理,更重要的是想思考一下广义线性模型的可解释性问题。由于平时的工作并不是做理论研究,我们的精算模型跑出来以后是要用在业务中的,会切实影响到我们客户每一单的保费折扣,为什么这个客户享受比较大的折扣,那个客户没有享受折扣呢?因为客户某一阶段的状态是高风险的(比如喜欢在凌晨时段出行、上年发生了事故造成了赔款等),因此不能给与折扣,进一步我们鼓励客户管理风险行为,进而下一年能享受折扣。我们需要和客户对话,让使用模型的人相信我们,让风险和价格匹配起来,这就是模型的可解释性的意义。
线性模型可以说是我们最熟悉的模型了,可以说是现实生活中最直接的因果关系。如果把模型比作是人的想法,线性模型就是“条件反射”,比如喝一口水会长胖一斤,和喝口水会长胖两斤,请问喝三口水长胖几斤?y=ax+b (本例中a=1,b=0),会长胖三斤,胖的非常线性。
非线性模型类似于人们更复杂的想法,添加了更多的约束和相互的影响。比如喝一口水长胖一斤,喝两口水要上一次厕所,所以可能只长胖1.414斤,喝四口水可能要上两趟厕所,运动一下还要出汗,因此可能只长胖2斤。 [公式] ,人的身体会新陈代谢,会自我调节,各方面的约束不会让你一直胖下去。这个模型开始考虑了一些现实的约束,添加进了人为活动的影响,模仿了稍微复杂一点的现象。
生活中还会有更复杂的影响机制,未来接触到的算法也会有更多更复杂的形式,但是我想他们都应该来源于现实,都是为了找到现实世界中的“规律”(或者说因果),因此一定是和现实相通的,我想在学习算法的过程可能也是我认知风险的过程吧~
2.广义线性模型的现实意义
前面说了线性模型与非线性模型的区别,那什么叫做广义线性模型呢?意思是在线性模型的基础上增加了其他约束。
首先,线性模型形式是这样的: y=β1x1+β2x2+……+βn+a,意思是 [公式]变化多少 x就相应比例的变化多少,但是这个模型存前提: x之间是不相关联的,y的特征分布受限(线性系统部分β1x1+β2x2+……+βn +高斯分布随机部分a )。比如 y用来描述车险的赔款金额,保险公司通常认为有相当一部分车辆发生的赔款金额是0,其余的赔款金额按照一定概率发生,如下图:
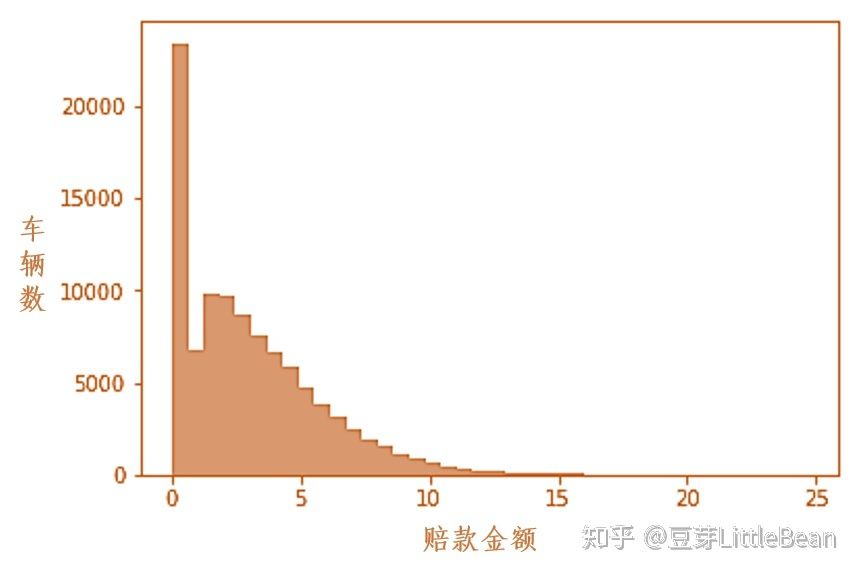
线性模型模拟出来的 y可能无法满足这样的分布,因此就无法准确的模拟现实中车险事故中的赔款,不符合车险事故的发生规律,此时需要对线性模型进行拓展,也就是广义线性模型。
3.指数分布族
指概率密度函数能写成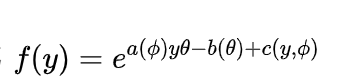 (或者
(或者 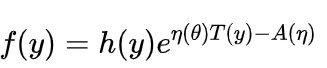 ,两种形式是一样的)的分布,主要有正态分布,伽马分布,二项分布,泊松分布,负二项分布等。
,两种形式是一样的)的分布,主要有正态分布,伽马分布,二项分布,泊松分布,负二项分布等。
广义线性模型中 Y的分布通常是指数分布族中的一种,逻辑回归模型中 Y 使用的伯努利分布就是指数分布族中的一种。本篇中车险索赔估计中 Tweedie分布也属于是指数分布族的一种。
为什么要使用指数分布族呢?个人觉得是因为指数分布族习形式在估计参数和损失函数方面更好处理。
4.广义线性模型的思路
还是以车险中的索赔金额 Y为例,我们认为 Y服从Tweedie分布,即 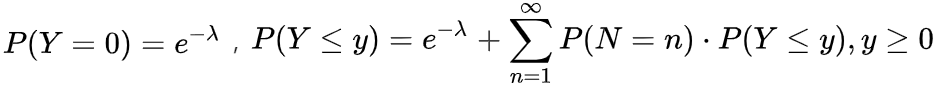 , 其概率密度函数为
, 其概率密度函数为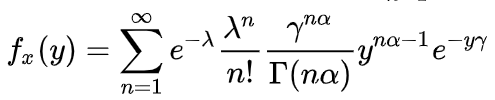 ,转换成指数分布族后(这个公式满足GLM模型中指数分布族的形式,公式比较复杂可以不看,就看成是描述索赔金额的数学公式就可以了)
,转换成指数分布族后(这个公式满足GLM模型中指数分布族的形式,公式比较复杂可以不看,就看成是描述索赔金额的数学公式就可以了)
也就意味着保险公司认为有相当一部分车是不会发生索赔的(索赔金额为0, Y=0 ),而在索赔金额大于0的情况下,服从一个连续分布,这个分布的形状有点像正态分布,索赔金额聚集在平均值附近,随着索赔金额的上升,发生的概率也在减小,还留着尾巴,从形状上来看比较符合车险事故的发生规律。具体步骤如下:
step1:确定描述对象(因变量)的分布——车险索赔金额选择Tweedie分布
step2:选择连接函数—— Tweedie分布选择对数为连接函数
step3:线性回归估计参数——建立特征值与目标值的关系估计出参数值
step4:模型检验——残差应该是均匀分布的
5.GLM模型可解释性的初步讨论(未来会针对GLM模型的可解释性做针对性的讨论)
我们模型评估出了结果,更关注的是这个结果在落地使用时会出现什么问题,这个时候可解释性就变得很重要。比如说我们的客户购买车险,可能价格非常高,比别的公司都要高,或者是被拒保了(拒绝承保),这个结果是出乎他意料的,自然而然的他会想知道为什么;再比如我们在购买物品或者观看视频的时候,相关的东西会推荐给我,比如电商给我推荐了手机壳,很可能是因为我购买了新手机。这就是可解释性的意义,很多的公司也都在增加市场策略的可解释性。
但模型有时候是不需要解释的,比如我们并不需要模型给出理由,而是给出惊喜(随机的结果哦),今天我不知道圣诞节去哪里吃饭,希望模型能随机给我一个建议,这时候并不需要理由;比如模型的效果已经被很好的验证,比如寄快递的地址识别已经很好的被很好的应用了,此时就不那么关心可解释性了;或者当模型给出了很好的解释性之后,使用的对象开始欺骗模型,人为去更改特征值操作系统,对模型的准确性造成损害。
关于模型的可解释性可以通过以下几个方面去思考:
公平性:确保模型违反价值导向、社会道德或者法律的偏见。由于模型是建立在样本数据基础之上建立起来的,不可避免的出现一些人口统计上的特征,比如地域或者性别等的特点,但是产品不能因为这些特点而进行歧视性的定价。
隐私性:确保数据中的敏感信息受到保护。
可靠性(稳健性):确保输入中的小变化不会导致预测发生大的变化。比如25岁的保费为5000元,26岁为1000元,差异过大一方面会让消费者产生疑惑,另一方面可能会让消费者瞒报年龄或者更改投保人。
模型改进:比如有些模型给一些因子赋予了比较大的权重,事实上这个因子只是碰巧有影响,对于因变量(被解释变量)并没有直接的因果关系,可解释性角度会删掉这个因子。
因果关系:与黑匣子相比,人类会选择相信有因果关系的市场行为,比如因为上一年出险了,所以下一年保费高。
6.GLM模型的缺陷
1、某些因子相关性较强的话会削弱其他因子的重要性
2、因变量与自变量之间关系本质上还是线性的
二、代码举例
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn import datasets,linear_model
## 导入数据
diabetes = datasets.load_diabetes() #使用 scikit-learn 自带的一个糖尿病病人的数据集
X_train,X_test,y_train,y_test=train_test_split(diabetes.data,diabetes.target,test_size=0.25,random_state=0)
## 建模
regr = linear_model.LinearRegression()
regr.fit(X_train, y_train)
print('Coefficients:%s, intercept %.2f'%(regr.coef_,regr.intercept_))
print("Residual sum of squares: %.2f"% np.mean((regr.predict(X_test) - y_test) ** 2))
print('Score: %.2f' % regr.score(X_test, y_test))
'''
-----------------------Tweedie------------------
'''
## 导入库函数
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn import datasets
from sklearn.linear_model import TweedieRegressor
## 导入数据
diabetes = datasets.load_diabetes() #使用 scikit-learn 自带的一个糖尿病病人的数据集
X_train,X_test,y_train,y_test=train_test_split(diabetes.data,diabetes.target,test_size=0.25,random_state=0)
## 建模
regr = TweedieRegressor(tol=0.0001,max_iter=5000,power=1.6,link='log',alpha=0.001)
regr.fit(X_train, y_train)
print('Coefficients:%s, intercept %.2f'%(regr.coef_,regr.intercept_))
print("Residual sum of squares: %.2f"% np.mean((regr.predict(X_test) - y_test) ** 2))
print('Score: %.2f' % regr.score(X_test, y_test))

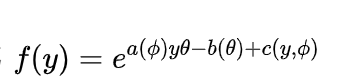 (或者
(或者 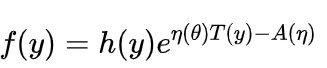 ,两种形式是一样的)的分布,主要有正态分布,伽马分布,二项分布,泊松分布,负二项分布等。
,两种形式是一样的)的分布,主要有正态分布,伽马分布,二项分布,泊松分布,负二项分布等。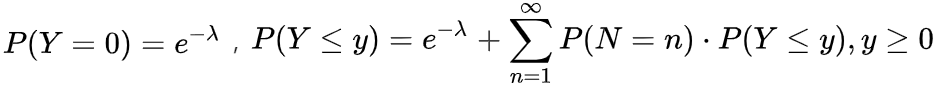 , 其概率密度函数为
, 其概率密度函数为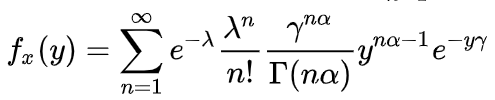 ,转换成指数分布族后(这个公式满足GLM模型中指数分布族的形式,公式比较复杂可以不看,就看成是描述索赔金额的数学公式就可以了)
,转换成指数分布族后(这个公式满足GLM模型中指数分布族的形式,公式比较复杂可以不看,就看成是描述索赔金额的数学公式就可以了)