不太常见的换算函数(Commutation function)
-
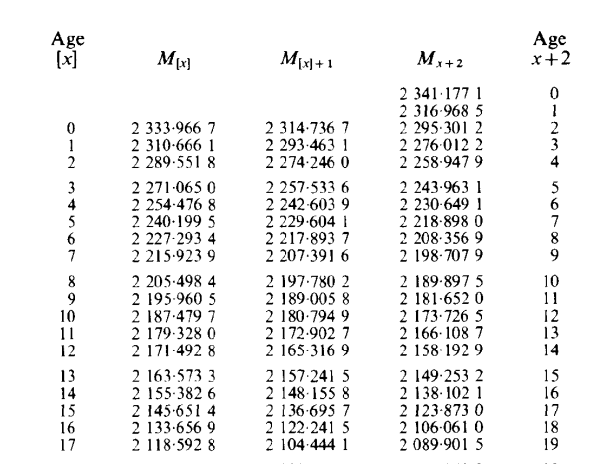
大家可能会思考 精算formula table AM92里面的$M$和$N$有什么作用。
答案是:它们可以被用作Commutation Function来使用$$\actsymb{}{}{A}{}{x:\angl{n}}=\frac{M_{x}-M_{x+n}}{D_{x}}$$
$$ \actsymb{}{}{A}{}{[x]:\angl{n}}=\frac{M_{x}-M_{x+n}}{D_{x}}$$
$$\actsymb{}{}{\ddot{a}}{}{x:\angl{n}}=\frac{N_{x}-N_{x+n}}{D_{x}}$$
$$\actsymb{}{}{\ddot{a}}{}{[x]:\angl{n}}=\frac{N_{[x]}-N_{x+n}}{D_{[x]}}$$
和下列commutation function 相比,它们更简单 但是更不精确
$$\actsymb{}{}{A}{}{x:\angl{n}}=\actsymb{}{}{A}{1}{x}- v^{n} \actsymb{n}{}{p}{}{x} \actsymb{}{}{A}{1}{x+n}$$
$$\actsymb{}{}{A}{}{[x]:\angl{n}}=A_{[x]}^{1}-v^{n} \actsymb{n}{}{p}{}{[x]} A_{x+n}^{1}$$
$$\actsymb{}{}{\ddot{a}}{}{x:\angl{n}}=\actsymb{}{}{\ddot{a}}{}{x}-v^{n} \actsymb{n}{}{p}{}{x} \actsymb{}{}{\ddot{a}}{}{x+n}$$
$$\actsymb{}{}{\ddot{a}}{}{[x]:\angl{n}}=\actsymb{}{}{\ddot{a}}{}{x}-v^{n} \actsymb{n}{}{p}{}{[x]} \actsymb{}{}{\ddot{a}}{}{x+n}$$
-
-
Formulae and tables 下载地址
https://www.actuaries.org.uk/system/files/documents/pdf/fullvolume.pdf
-
这个现在也就只有理论意义了吧。。。现在工作还用得着换算函数吗??计算能力都上来了,Excel算一下不就行了?
-
@Nothanks 嗯嗯 目前是理论意义大于实际意义,但是有的精算考试中还需要。希望能理论能跟上实际的步伐吧
